Opérations
sur les fractions
En Sixième, tu as sans doute déjà
additionné, soustrait ou multiplié deux fractions. Il s'agissait alors de
fractions sur 10, 100 ou 1000.
Le traitement que tu réservais à ces fractions décimales, nous allons
l'étendre à toutes les autres. Et à la fin, nous les combinerons...
Additionner et soustraire deux fractions.
Ce premier
Comme nous allons le voir, additionner deux fractions revient à ajouter des
parts de gâteaux.
Pour bien comprendre et analyser le phénomène, nous allons devoir envisager
deux cas de figure.
- Les deux fractions ont même
dénominateur.
Par exemple, additionnons les fractions  et
et  .
.
 |
Parlons tout de suite de ce qu'il ne
faut pas faire !
Certains petits malins diront
certainement que pour additionner deux fractions, il suffit d'ajouter
séparément leurs numérateurs et leurs dénominateurs !
En clair, ils feront la bêtise suivante :
 C'est une belle
anerie car 0,25 + 0,5 est égal à 0,75. Et non à 0,375 ! C'est une belle
anerie car 0,25 + 0,5 est égal à 0,75. Et non à 0,375 !
Donc ce n'est certainement pas ainsi qu'il faut faire ! |
Envisageons les choses de manière plus
gastronomique !
Rapportées à un gâteau rond partagé en quatre parts, la
fraction  représente une part et
représente une part et  correspond à 2 parts.
correspond à 2 parts.
Comme nous devons faire une addition, additionnons les parts !
Nous avons donc la situation suivante :

Inspirons-nous de cet exemple gourmand.
La bonne manière d'additionner les fractions  et
et  est donc :
est donc :
 Comme
Comme
 est égal à 0,75 , nous avons donc trouvé le bon résultat !
est égal à 0,75 , nous avons donc trouvé le bon résultat !
Nous savons désormais comment additionner (et même soustraire) deux
fractions ayant le même dénominateur.
Cette règle est certes utile mais que se
passe-t-il lorsque les deux fractions n'ont pas le même dénominateur ?
C'est l'objet du cas suivant.
Les deux fractions n'ont pas le
même dénominateur.
Par exemple, additionnons les fractions  et
et  .
.
Représentons pâtissièrement cette addition :
 A quelle fraction correspond la part totale ? Voilà la question !
A quelle fraction correspond la part totale ? Voilà la question !
Les quarts et les tiers ne s'additionnent pas facilement même lorsqu'il
s'agit de parts de gâteau !
La seule chose que nous savons faire est d'additionner deux fractions ayant
le même dénominateur.
Nous allons donc mettre les fractions  et
et  sur un même dénominateur.
sur un même dénominateur.
Parmi les dénominateurs communs possibles, il y a 12, 24, 36...
Nous choisissons le plus simple d'entre eux qui est 12.
La situation vient donc évolué : au lieu
d'additionner des quarts et des tiers, nous additionnerons des douzièmes...

La bonne manière d'additionner les fractions  et
et  est donc :
est donc :

Pour additionner (ou soustraire) deux fractions n'ayant pas le même
dénominateur, il suffit de leur trouver un dénominateur commun. D'où la
règle suivante :
Règle 2 : additionner (ou
soustraire) deux fractions ayant des dénominateurs différents.
Pour additionner (ou soustraire) deux fractions n'ayant pas le
même dénominateur :
- on les met sur un même
dénominateur.
- puis, on les additionne (ou on les
soustrait) en utilisant la règle 1.
|
Nous savons désormais comment additionner ou
soustraire deux fractions grâce à nos deux règles. Mais rien ne remplace la
pratique !
C'est l'objet du prochain paragraphe.
Addition
ou soustraction particulières.
Dans le précédent paragraphe, nous
avons vu et expliquer les règles qui permettent d'additionner et de soustraire
deux fractions.
Dans ce paragraphe, nous allons la mettre en pratique sur deux exemples
particuliers.
Exemple 1 : le plus petit
dénominateur commun.
Effectuons l'opération  . .
Pour soustraire ces deux fractions, il faut au préalable leur trouver
un dénominateur commun.
Certains diront que leur dénominateur commun est 48
= 8 × 6.
C'en est un mais ce n'est pas le plus simple !
Le plus simple est 24
car 24 = 8 × 3 et 24 = 6 ×
4.

Nous aurions pu faire le
calcul en choisissant pour dénominateur commun 48 mais ils auraient été
un peu plus compliqués... |
Exemple 2 : additionner un entier et
une fraction.
Par exemple, effectuons l'opération  . .
Là, il y en a qui vont dire : "Additionner deux entiers, on sait
faire. Additionner des fractions, on sait faire. Mais additionner un
entier et une fraction, on ne sait pas faire !
Erreur car un entier est une fraction qui
s'ignore ! En effet,  . .
A partir de là, nous savons faire !

Ce que nous avons fait pour
l'entier 3 peut être refait pour n'importe quel nombre décimal car un
décimal est lui aussi une fraction qui s'ignore. |
Multiplier deux fractions.
Contrairement à l'addition et à la
soustraction, les fractions se passent très bien le cap de la multiplication.
Peut-être est-ce parce que une fraction est avant tout une division...
Règle : multiplier deux fractions.
Le produit de deux fractions est la fraction dont :
- le numérateur
est le produit des deux numérateurs des deux facteurs.
- le dénominateur
est le produit des deux dénominateurs de deux facteurs.
Autrement écrit :

|
Ainsi par exemple :
 Nous savons multiplier deux entiers ou deux fractions. Mais qu'en est-il de la multiplication d'une entier par une fraction ?
Nous savons multiplier deux entiers ou deux fractions. Mais qu'en est-il de la multiplication d'une entier par une fraction ?
Le problème : multiplier un
entier et une fraction.
Par exemple, effectuons la multiplication 3 ×  . .
A l'opération près, c'est l'exemple 2
du précédent paragraphe.
Nous avions usé alors d'une grosse astuce en disant que l'entier 3
était aussi la fraction  . .
Réutilisons cette astuce...
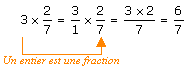
Une remarque :
Si l'on regarde bien ce qui a été fait, on observe que :
- on a multiplié le numérateur 2 par l'entier 3.
- on a conservé le dénominateur 7.
C'est l'application de la règle :

|
Des additions, des soustractions et des
multiplications : la totale !
Dans une expression, il est possible d'avoir trois fractions, une addition
et une multiplication. Par exemple, nous pourrions être amené à
calculer  .
.
Point de panique car ce genre de calculs, nous savons les faire. C'est juste une
histoire de priorités opératoires.
Voyons comment marchent les choses avec deux
exemples :
- Calculons
 .
.
Cette expression se compose d'une addition et d'une multiplication. Cette
dernière est prioritaire sur la première. Le calcul commencera donc par la
multiplication.

- Calculons
 .
.
La présente expression comporte une multiplication et une addition entre
parenthèses. Nous devons en priorité nous occuper de ce qui est entre
parenthèses.

Une remarque de présentation dans
tes calculs :
A l'issue d'un calcul, on s'arrange (et t'arrangeras) toujours
pour donner la fraction la plus simple possible. C'est-à-dire celle ayant
les plus petits numérateur et dénominateur possibles. |
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) Mai 2000/Janvier 2003. Tous droits réservés.

 et
et  .
.

 représente une part et
représente une part et  correspond à 2 parts.
correspond à 2 parts.
 et
et  est donc :
est donc :
 est égal à 0,75 , nous avons donc trouvé le bon résultat !
est égal à 0,75 , nous avons donc trouvé le bon résultat ! et
et  .
.
 et
et  sur un même dénominateur.
sur un même dénominateur.


 est donc :
est donc :

 .
.
 .
. .
.


 .
.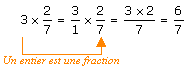

 .
.
 .
.