 La réponse La réponse |
Quelques mots pour terminer  |
|
Une introduction à la notion de fonction
- On a défini une fonction ! -
Comme l'indique le titre de cette page, nous venons sans le savoir de définir une fonction ! Cette fonction est la fonction Aire(.) dont la variable est x. Rappelons que x représente la position de N sur le segment [AC].
Cette fonction Aire est un procédé qui lie la position de N sur [AC] à l'aire du rectangle (MNPB). Autrement exprimé, c'est un procédé qui à chaque x fait correspondre un réel qui est l'aire de (MNPB).
De plus, parler de l'aire de (MNPB) n'a de sens que dans la mesure où N est sur le segment [AC], donc que dans la mesure où x est compris entre 0 et 5. On dit alors que l'ensemble de définition de la fonction Aire est l'intervalle [0 ; 5]. C'est-à-dire que c'est l'ensemble de définition pour lesquels la fonction Aire est définie.
De plus si x = 2 alors l'aire du rectangle (MNPB) est égale à 2,88. On dit alors que 2,88 est l'image de 2 par la fonction Aire.
Tout cela peut être résumé par :
Courbe représentative d'une fonction.
On représente toute fonction par une courbe représentation graphique. On parle aussi de courbe représentative. L'avantage d'une courbe est que c'est nettement plus concret qu'une fonction !
La courbe représentative de la fonction Aire est l'ensemble des points M(x ; f(x)) lorsque x décrit [0 ; 5]. C'est l'ensemble de définition de la fonction Aire.
Pour construire cette courbe, on procède de la manière suivante :

Remarque :
Une fonction peut aussi être définie au moyen de sa représentation graphique comme nous le verrons dans la suite.
Comment déterminer l'image d'un réel.
La réponse à cette question dépend des renseignements dont on dispose.
Si l'on dispose d'une formule explicite comme c'est ici le cas alors pour calculer l'image de 2, il suffit de remplacer x par 2.
A titre d'exemple, calculons l'image de certains réels x par cette fonction.
Si l'on dispose de la seule courbe représentative alors on peut faire comme il suit :

Antécédent : définition et comment les déterminer ?
Une autre question que l'on peut se poser est de savoir pour quelles valeurs de x, l'aire est égale à 2. On dit alors que l'on recherche les antécédents de 2.
Plus précisément, on recherche quels sont les réels x compris entre 0 et 5 qui ont pour image 2 par la fonction Aire.
Comme nous le verrons par la suite, un réel peut avoir 0, 1, 2 voir une infinité d'antécédent. A la différence de l'image, l'antécédent n'est pas toujours unique. Il y a même des fois où il n'existe pas !
Une question que l'on peut se poser est : comment peut-on déterminer les antécédents de 2 par cette fonction Aire ?
Là comme pour les images, deux réponses sont possibles selon ce que l'on sait de cette fonction.
Si l'on dispose de la formule explicite comme c'est ici le cas, savoir quels réels x de l'intervalle [0 ; 5] ont pour image 2 par la fonction Aire revient à résoudre dans l'intervalle [0 ; 5] l'équation Aire(x) = 2. Les antécédents de 2 sont les solutions de cette équation. Autant de solutions que d'antécédents...
La résolution de cette équation est la suivante :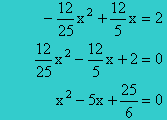
x2 - 5x est le début d'une identité (ou égalité) remarquable. Faisons-la apparaitre !
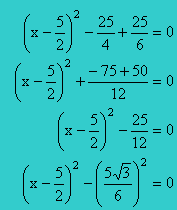
Nous avons une différence de deux carrés. Or a2 - b2 = (a - b) (a + b). Ainsi :
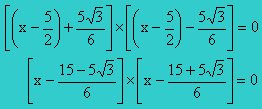
Or un produit de deux facteurs est nul si et seulement si l'un des facteurs est nul. Ainsi :
![]()
![]()
Or ces deux réels fonct partie de [0 ; 5] (c'est l'ensemble de définition de la fonction Aire).
![]()
L'applette suivante recherche les antécédents de n'importe quel réel.
De quel réel faut-il rechercher le ou les antécédents par la fonction Aire ?
Si l'on ne dispose que de la représentation graphique de cette fonction, il faut alors procéder comme suit :

|