Ce
qui est le plus intéressant dans cet exercice sont les calculs qui
permettent l'élabroration du tableau de signe de la fraction.
Pour ceux qui auraient du
mal à voir pourquoi il en est ainsi, nous allons détailler
le travail fait !
Cette fraction est le quotient
du réel -2 et
de l'expression (x + 3).(x + 5).
Si
l'on connait le signe du numérateur et celui du dénominateur
suivant x alors on peut en déduire
le signe de la fraction.
Signe
du numérateur -2.
Cela
peut paraitre bête à dire mais le signe du numérateur
-2
est toujours négatif et ce quelque soit x.
Son
tableau de signe est donc :

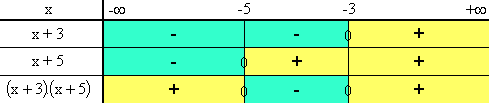
Signedu dénominateur (x + 3).(x + 5).
Le
dénominateur est un produit de deux binômes de la forme a.x
+ b. Les facteurs sont :
-
x +
3 où a = 1
et b = 3.
-
x +
5 où a = 1
et b = 5.
Le tableau
de variation du produit est donc le suivant :
Conclusion: signe de la fraction.
Nous
connaissons les signes des numérateur et dénominateur suivant
x, nous allons pouvoir en déduire celui de leur quotient.
Le
tableau de signe de la fraction est :

Quelques commentaires sur ce
tableau :
Au vu du tableau de signe
du dénominateur, on entrevoit les différents cas qu'il faut
envisager. Gardons toujours présent à l'esprit que le numérateur
-2 est toujours négatif.
-
avant
-5,
le dénominateur (x + 3).(x
+ 5) est positif. Donc la fraction
est négative.
-
lorsque
x vaut -5,
le dénominateur (x + 3).(x
+ 5) est nul. Donc la fraction n'existe pas.
-
entre
-5
et -3,
le dénominateur (x + 3).(x
+ 5) est négatif. Donc la
fraction est positive.
-
lorsque
x vaut -3,
le dénominateur (x + 3).(x
+ 5) est nul. Donc la fraction n'existe pas.
-
après
-3,
le dénominateur (x + 3).(x
+ 5) est positif. Donc la fraction
est négative.
Cette page ainsi que la quasi-totalité des éléments et de la programmation qui la composent ou qui en dépendent, ont été conçus et réalisés par Jérôme ONILLON. Elle est exclusivement mise en ligne par
la taverne de l'Irlandais.
(c) AMLTI Juin 1999/Janvier 2003. Tous droits réservés.




