
S'il y a une chose à ne surtout pas faire, c'est développer car cela ne conduit à rien d'exploitable...
Résoudre cette équation revient
en fait à savoir pour quelles valeurs de x, l'expression
Or, il y a là un produit de deux binômes de la forme a.x
+ b.
Comme l'on connait le signe de chacun des deux facteurs
en fonction de x, alors on peut en déduire le signe de leur produit
!
Au boulot :
Le facteur 7.x + 5 est un binôme de la forme a.x + b où a = 7 et b = 5. Son tableau de signe est donc :

Le facteur 2 - 3.x est un binôme de la forme a.x + b où a = -3 et b = 2. Son tableau de signe est donc :

Connaissant le signe de chacun des deux facteurs, nous pouvons déterminer
le signe du produit
Pour cela, on rassemble les deux tableaux précédents
dans un plus grand tableau. Et on applique...
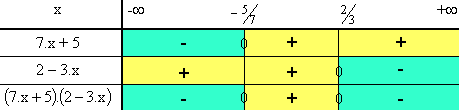
Le produit est positif entre -5/7
et 2/3 non
compris. L'ensemble des solutions de l'inéquation est donc :